EdgarStat® contains an internal regression model to calculate the beta-risk coefficient of an individual enterprise stock price return compared to the return of the S&P 500 stock price (market) index. This stock price return regression model is known as CAPM.
Let the individual stock price return be calculated with the investment gain or loss formula:
(1) R(t) = {[P(t) / P(t − 1)] – 1}, such that we postulate the linear relation:
(2) Y(t) = α + β M(t)
where the dependent variable is Y(t) = [R(t) + 1] = [P(t) / P(t − 1)] or P(t) = [1 + R(t)] P(t − 1).
The variable M(t) is the stock market price return, measured using the same eq. (1).
In eq. (2), the intercept (= α) is the adjusted stock price return, equivalent to the local short-term sovereign bill return. Some call the intercept “seeking alpha." The slope coefficient (= β) is the derivative of the individual stock price return with respect to the stock market price (index) return.
In EdgarStat, we use monthly R(t) to calculate α, β, and σ = √Var(Y(t)) for individual companies selected by the user. It’s sensible to calculate (2) using quarterly data, because dividends are reported per quarter of year.
Example 1: The CAPM Coefficients of Chevron Corp. (GVKEY 2991, Mergent 7846)
(5) Y(t) = 0.8379 M(t) – 0.111, σ = 6.2558
where σ is the residual standard error.
The intercept is not significant (Newey-West t-Statistics are –0.3893), and the slope coefficient is significant with the Newey-West corrected t-Statistics = 11.2001. Count = 490 observations from 2023-01-1 back to 1982-01-31. The R2 = 25.45%, showing that for Chevron the CAPM linear model is a bad fit.
Example 2: The CAPM Coefficients of ConocoPhillips (GVKEY 8549, Mergent 6630)
(3) Y(t) = 1.017 M(t) – 0.1052, σ = 8.2715
The intercept is not significant (Newey-West t-Statistics are –0.2761), and the slope coefficient is significant with the Newey-West corrected t-Statistics = 9.4952. Count = 490 observations from 2023-01-1 back to 1981-12-31. The R2 = 22.34%, showing that for ConocoPhillips the CAPM linear model is a bad fit.
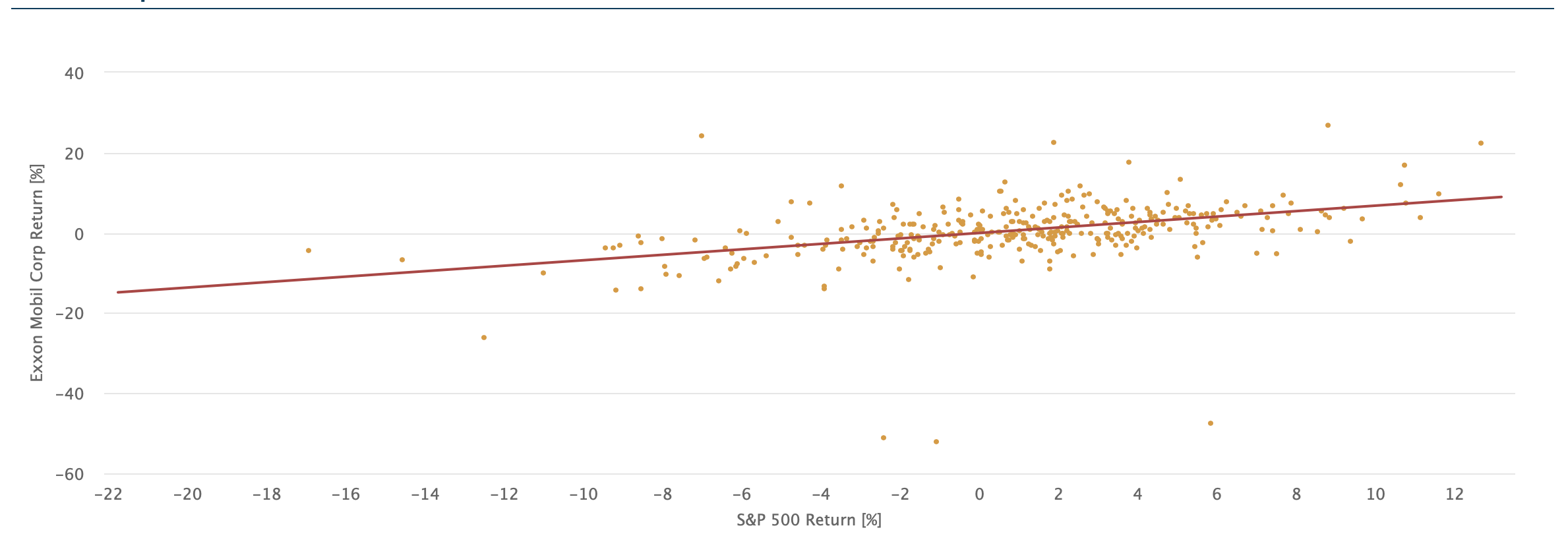
Example 3: The CAPM Coefficients of Exxon Mobil Corp. (GVKEY 4503, Mergent 7846)
(4) Y(t) = 0.681 M(t) – 0.0189, σ = 6.285
The intercept is not significant (Newey-West t-Statistics are –0.0642), and the slope coefficient is significant with the Newey-West corrected t-Statistics = 8.0272. Count = 490 observations from 2023-01-1 back to 1982-01-31. The R2 = 18.26%, showing that for Exxon Mobil the CAPM linear model is, again, a bad fit.
The principal takeaway is that canned beta coefficients are unreliable to discount the expected future stock prices of a selected enterprise to the present. Also, canned beta coefficients are an unreliable measure of risk.
References
Richard Brealey & Stewart Myers, Principles of Corporate Finance (6th edition), McGraw-Hill, 2000, § 8.2 (Relationship between risk and return) and § 9.1 (Measuring betas).
Zvi Bodie & Robert Merton, Finance, Prentice Hall, 2000, § 13.3 (Beta and risk premiums on individual securities).
Chart 1: Chevron Corp. (GVKEY 2991, Mergent 7846)
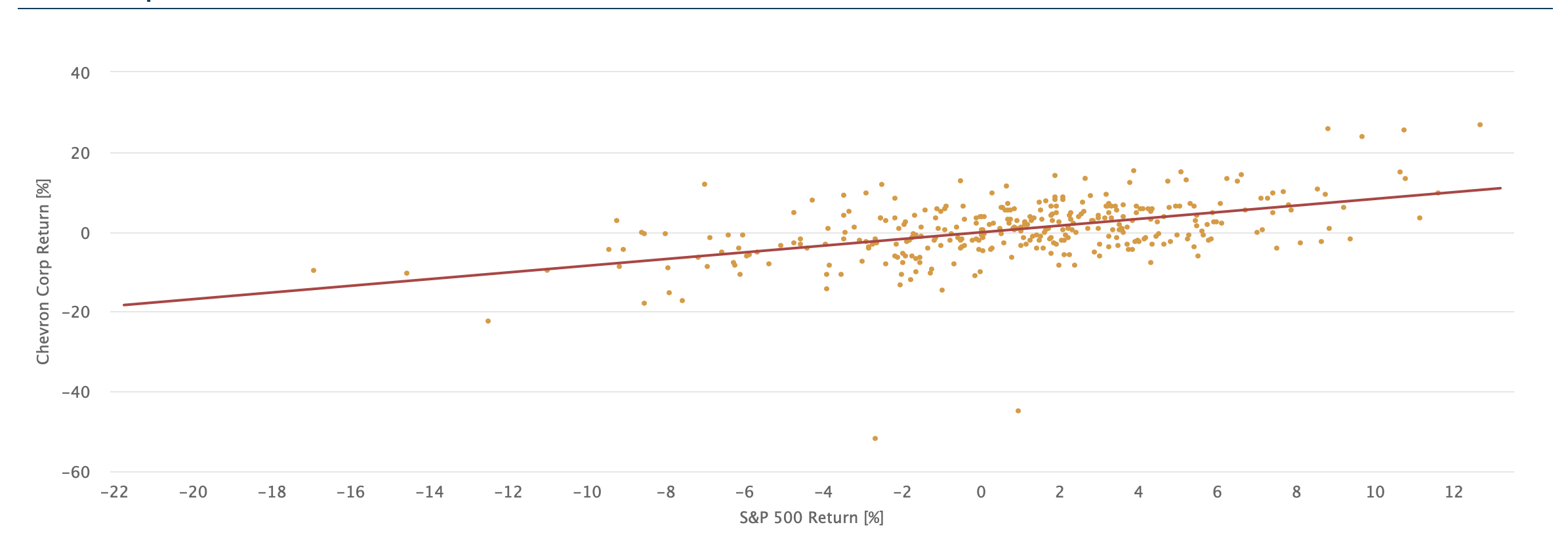
Chart 2: ConocoPhillips (GVKEY 8549, Mergent 6630)
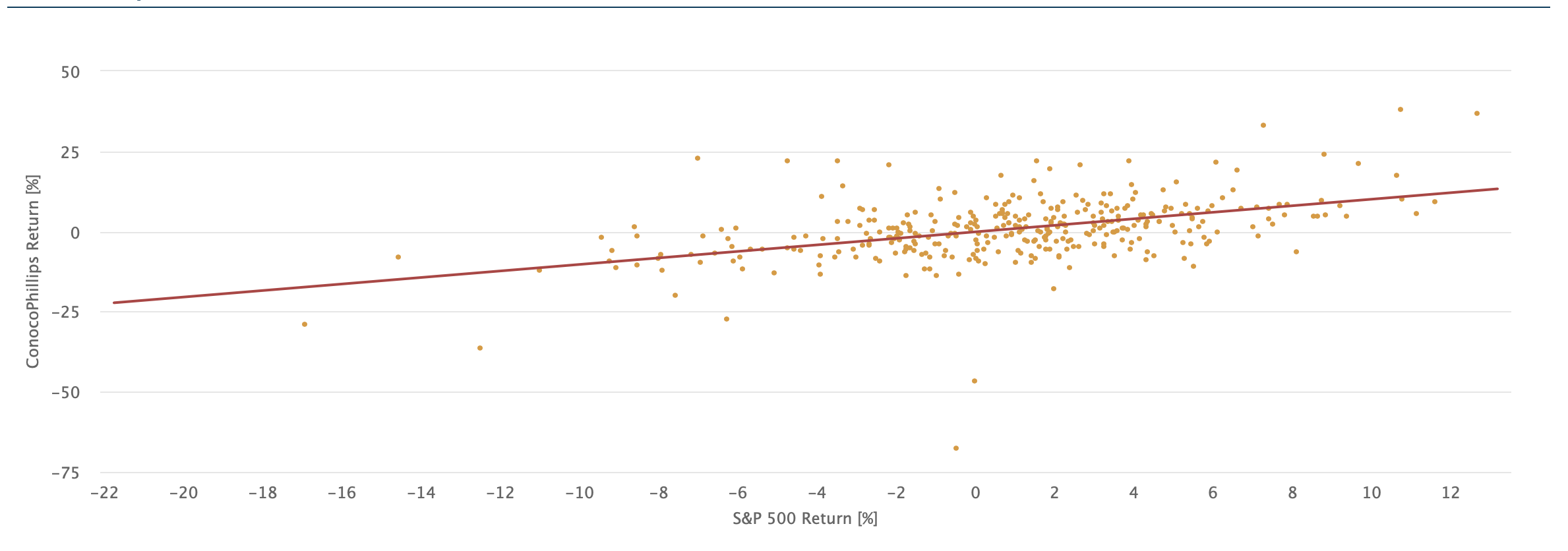
Chart 3: Exxon Mobil Corp. (GVKEY 4503, Mergent 7846)
